ch6 神经网络
总览
- 单层感知机网络
- 单层感知机网络的学习规则
- 多层感知机
- 反向传播学习算法
- 径向基函数网络
- 自组织映射
导入
- 神经网络是一种受大脑执行特定学习任务方式启发的机器学习方法:
- 关于学习任务的知识以示例的形式给出。
- 神经元间的连接强度(权重)用于存储所获取的信息(训练示例)。
- 在学习过程中,权重会被修改,以便在训练示例上正确地对特定学习任务进行建模。
- 涉及到
- 各种类型的神经元
- 各种网络架构
- 各种学习算法
- 各种应用
神经网络的特征
- 大规模和并行处理
- 稳健性
- 自适应和自组织
- 足以模拟非线性关系
- 硬件实现
结构
- 前馈
- 反馈
学习方法
- 有监督
- 无监督
信号类型
- 连续
- 离散
感知机
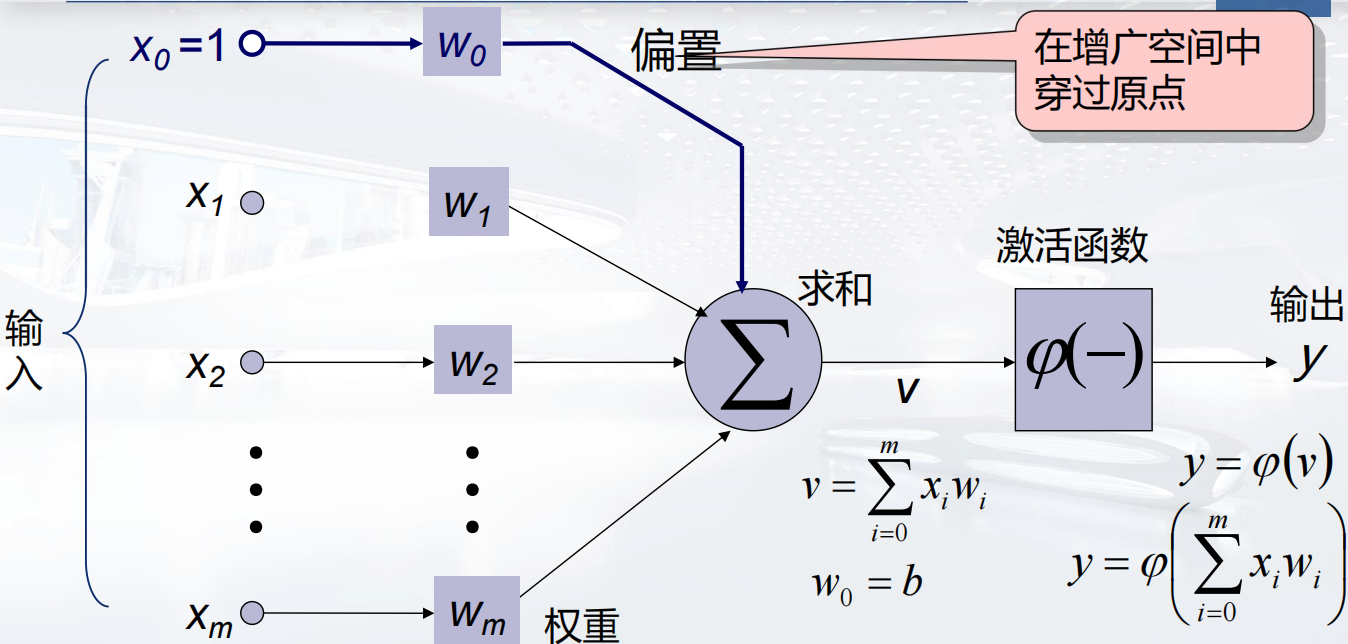 计算方式如图所示 不多说了
计算方式如图所示 不多说了
激活函数
分为连续的激活函数和离散的激活函数,用于将输入信号转换为输出信号。
线性可分
线性可分是指在一个数据集中,存在一个超平面(在二维空间中是一条直线,在更高维空间中是一个平面或更高维的线性结构),能够将不同类别的数据点完全分开,使得同一类别的数据点都在超平面的一侧,而不同类别的数据点在超平面的另一侧。
所有的感知机基于线性可分的前提,即数据集中的每个类别都可以通过一个超平面完全分开。
感知机学习机制
目标是
更新规则:
如何更新权重向量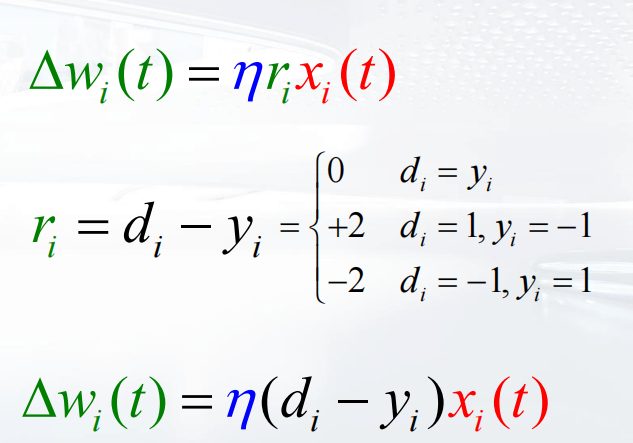 其中
其中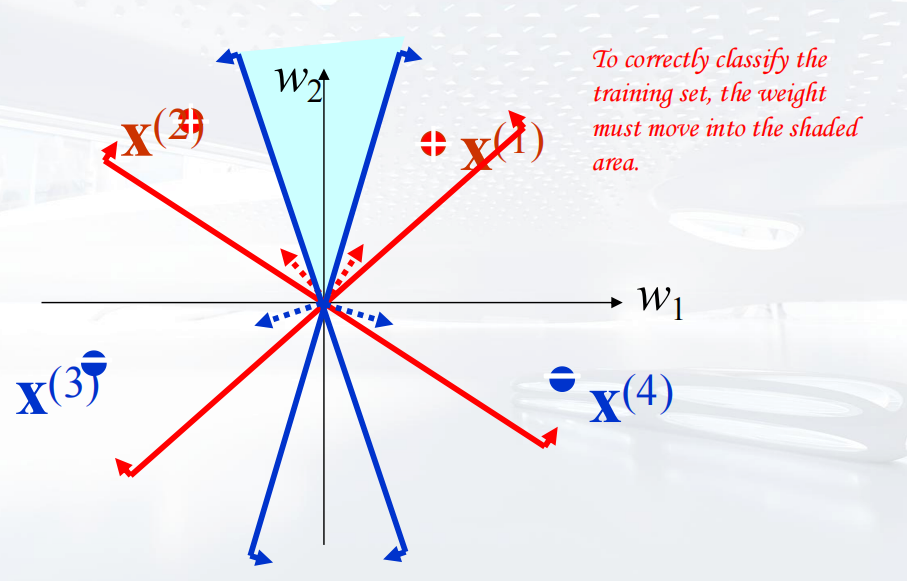 正确的的权重位置应该落在反例向量反方向,正例向量正方向的区域并集里,如图所示。
正确的的权重位置应该落在反例向量反方向,正例向量正方向的区域并集里,如图所示。
通过不断的迭代,最后让权重向量落在正确的位置,从而完成学习。
如何最快下降:
肯定是沿着梯度方向函数值下降最快呀。

梯度与权重向量的内积决定了权重向量移动的方向和距离。

学习模式
- 批量学习模式
- 增量学习模式
- 批量学习是使用整个训练集计算梯度更新模型参数,而增量学习是每次用一个或一小批数据样本来更新模型参数。
总结
- 可分性:某些参数能使训练集完全正确分类。
- 收敛性:如果训练集是可分的,感知机最终会收敛(二分类情况)?
多层感知机
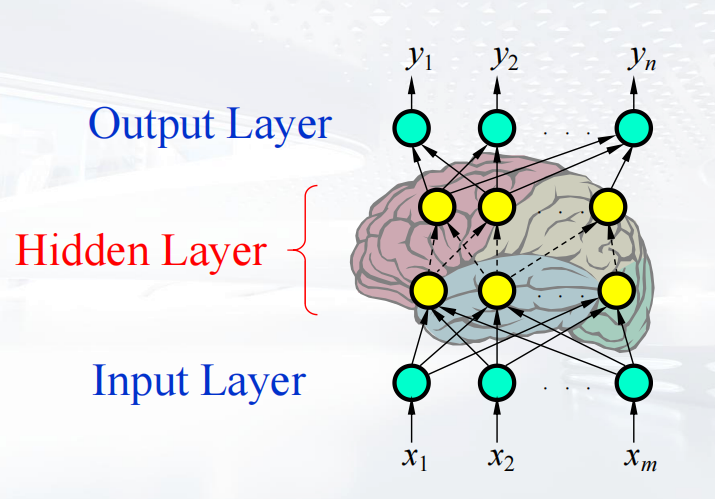
反向传播算法(BP算法)
推导过程简直就不是人类能理解的,直接看结论
反向传播算法(Back propagation,简称BP算法)是“误差反向传播”的简称,是适合于多层神经元网络的一种学习算法,它建立在梯度下降法的基础上。梯度下降法是训练神经网络的常用方法,许多的训练方法都是基于梯度下降法改良出来的,因此了解梯度下降法很重要。梯度下降法通过计算损失函数的梯度,并将这个梯度反馈给最优化函数来更新权重以最小化损失函数。
一共有两个步骤:
- 计算误差
- 误差反向传播
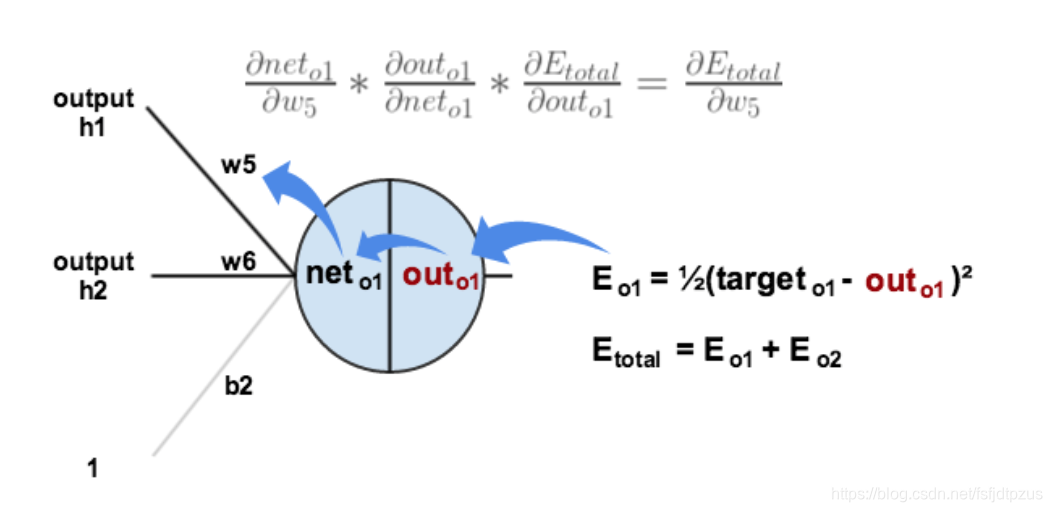
计算误差
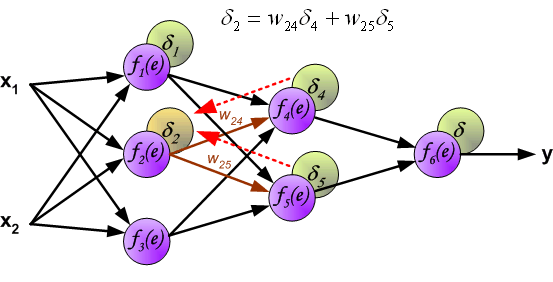
第一步是计算神经网络的输出(预测值)和真值的误差 图中y为我们神经网络的预测值,由于这个预测值不一定正确,所以我们需要将神经网络的预测值和对应数据的标签来比较,计算出误差。误差的计算有很多方法,比如上面提到的输出与期望的误差的平方和,熵(Entropy)以及交叉熵等。计算出的误差记为δ。 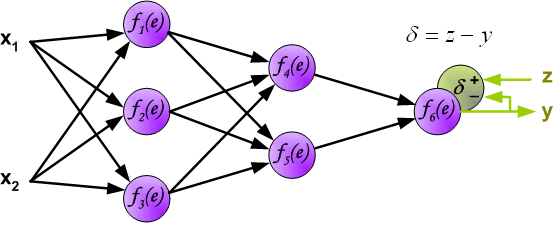 反向传播,顾名思义,是从后向前传播的一种方法。因此计算完误差后,需要将这个误差向不断的向前一层传播。向前一层传播时,需要考虑到前一个神经元的权重系数(因为不同神经元的重要性不同,因此回传时需要考虑权重系数)。
反向传播,顾名思义,是从后向前传播的一种方法。因此计算完误差后,需要将这个误差向不断的向前一层传播。向前一层传播时,需要考虑到前一个神经元的权重系数(因为不同神经元的重要性不同,因此回传时需要考虑权重系数)。 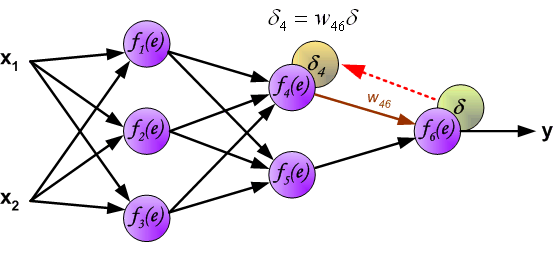
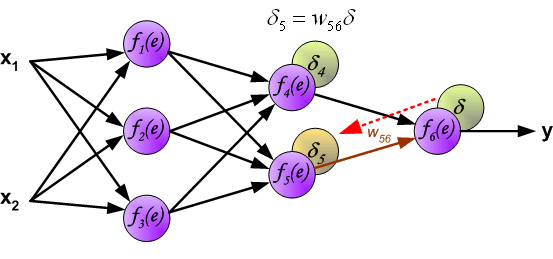 与前向传播时相同,反向传播时后一层的节点会与前一层的多个节点相连,因此需要对所有节点的误差求和。
与前向传播时相同,反向传播时后一层的节点会与前一层的多个节点相连,因此需要对所有节点的误差求和。 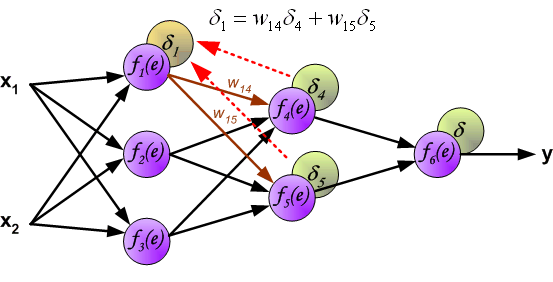
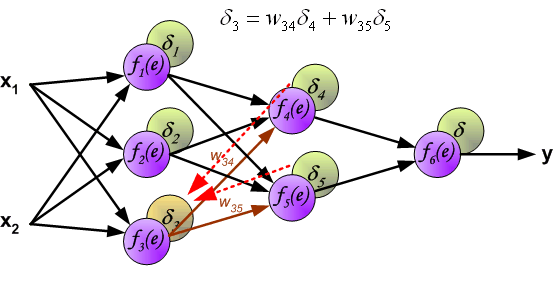
更新权重
图中的η代表学习率,w′是更新后的权重,通过这个式子来更新权重。这个式子具体是怎么来的,请看下面的具体事例,现在只要先保留大概的印象就行了。 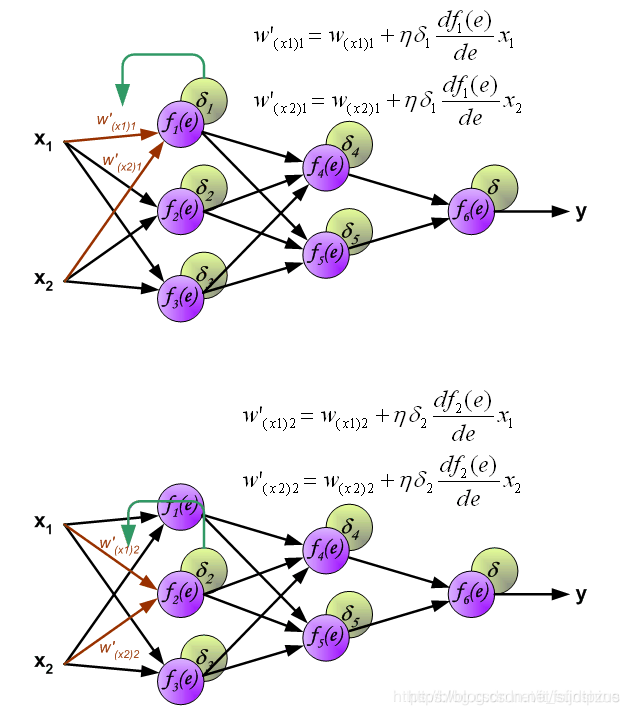
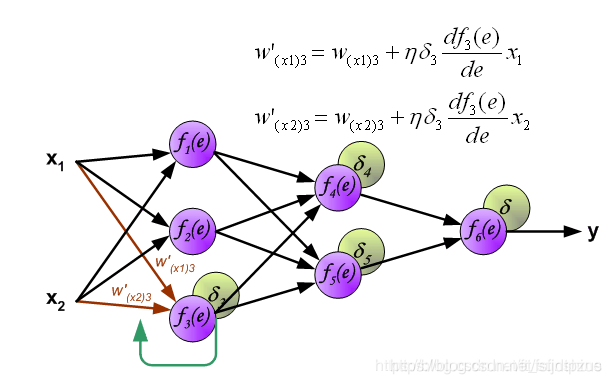
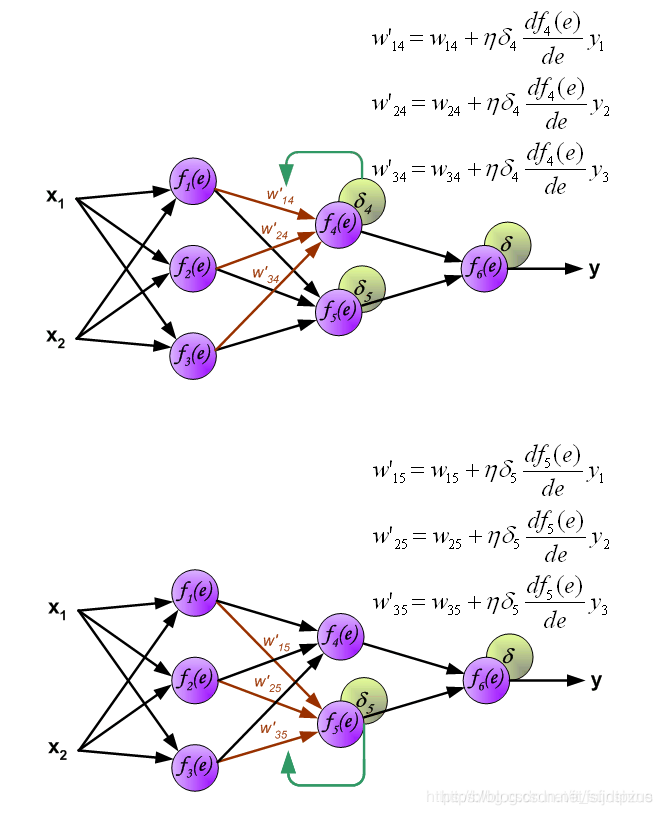
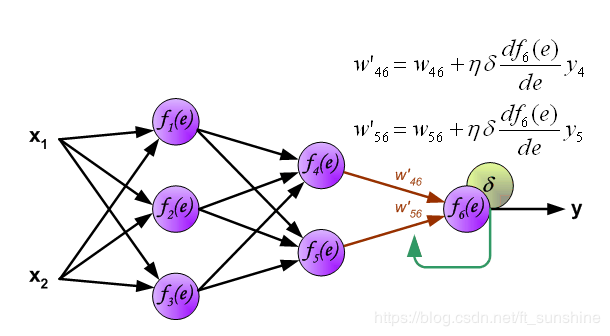
举个栗子
学习率
- 一般来说,反向传播(BP)无法被证明是收敛的,并且没有明确界定的停止其操作的标准。
- 然而,有一些合理的标准可用于终止权重调整,例如:
- 当梯度向量的欧几里得范数达到足够小的梯度阈值时。
- 当每个轮次的平均平方误差足够小时。通常,它在每个轮次的0.1%到1%的范围内,或者小到0.01%。
输入归一化
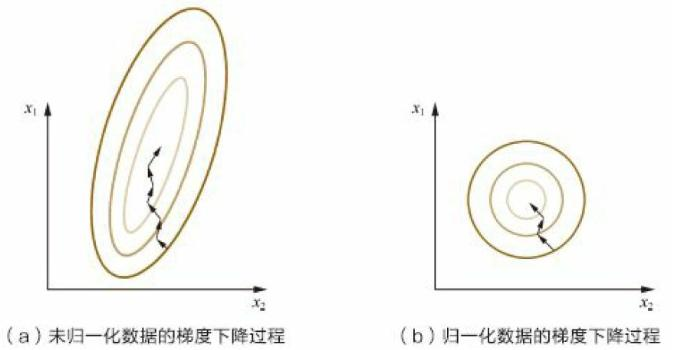
- 最大最小归一化和Z-score归一化

反向传播(BP)学习的优点
- 强大的表示能力
- 广泛的实际应用性
- 易于实现
- 良好的泛化能力
反向传播(BP)学习的问题
- 学习往往需要很长时间才能收敛
- 网络本质上是一个黑盒?
- 梯度下降方法仅能保证局部最小误差
- 不是每个可表示的函数都能被学习
- 即使误差降为零,泛化也不能保证
初始化
- 过大
- 网络中的神经元将被驱动到饱和状态。
- 过小
- BP 算法将在误差曲面原点周围的一个非常平坦的区域上运行。
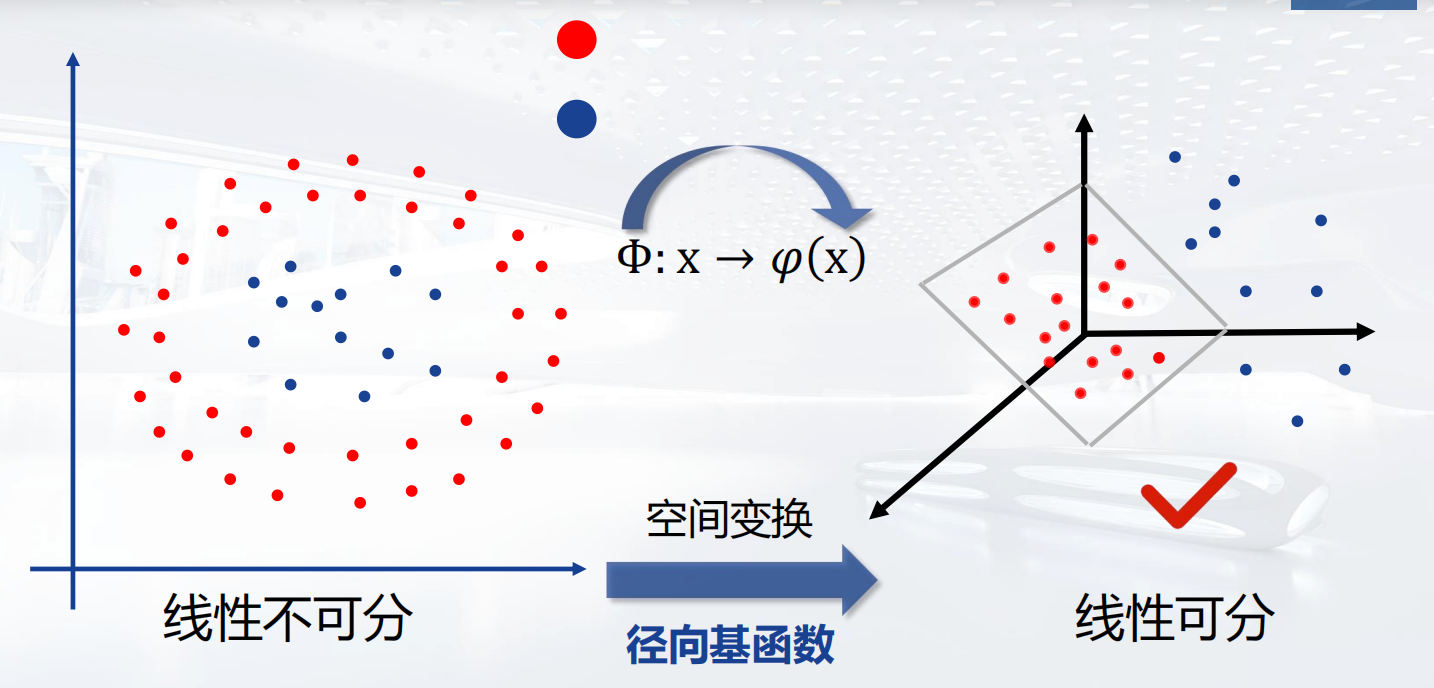
径向基函数网络
径向基函数 (RBF,Radial Basis Function) 是一个取值仅取决于输入点到中心点(原点)距离的实值函数。 
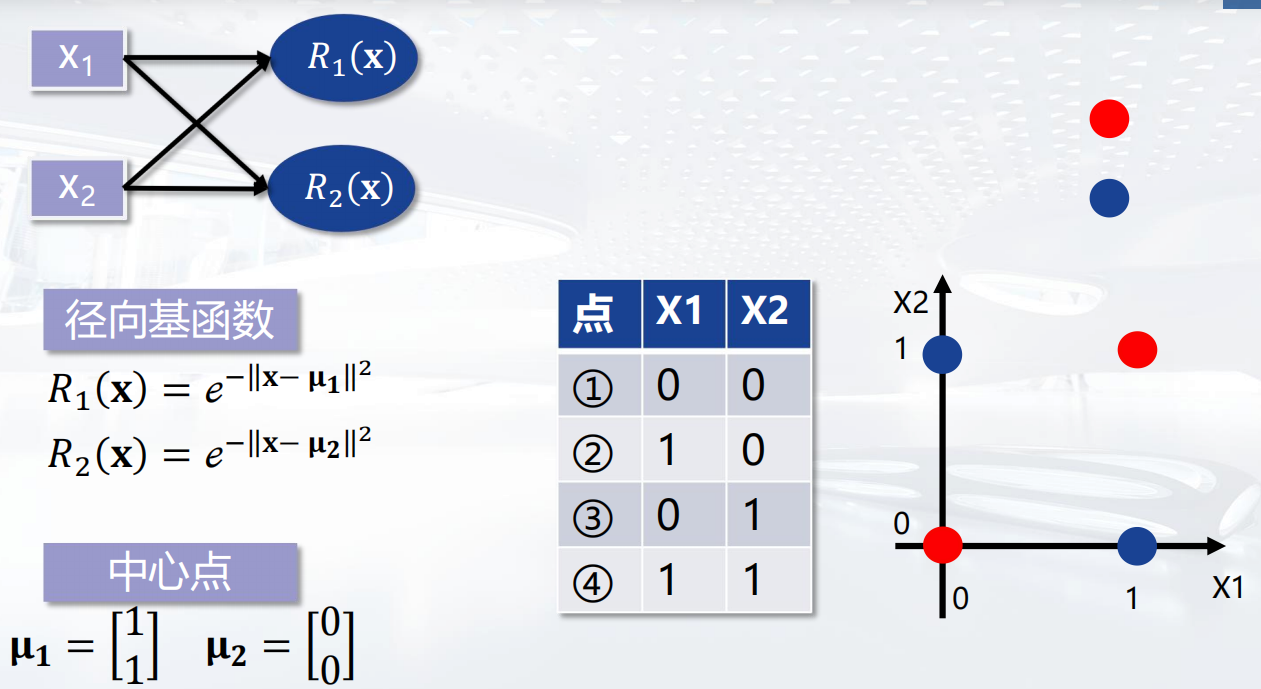

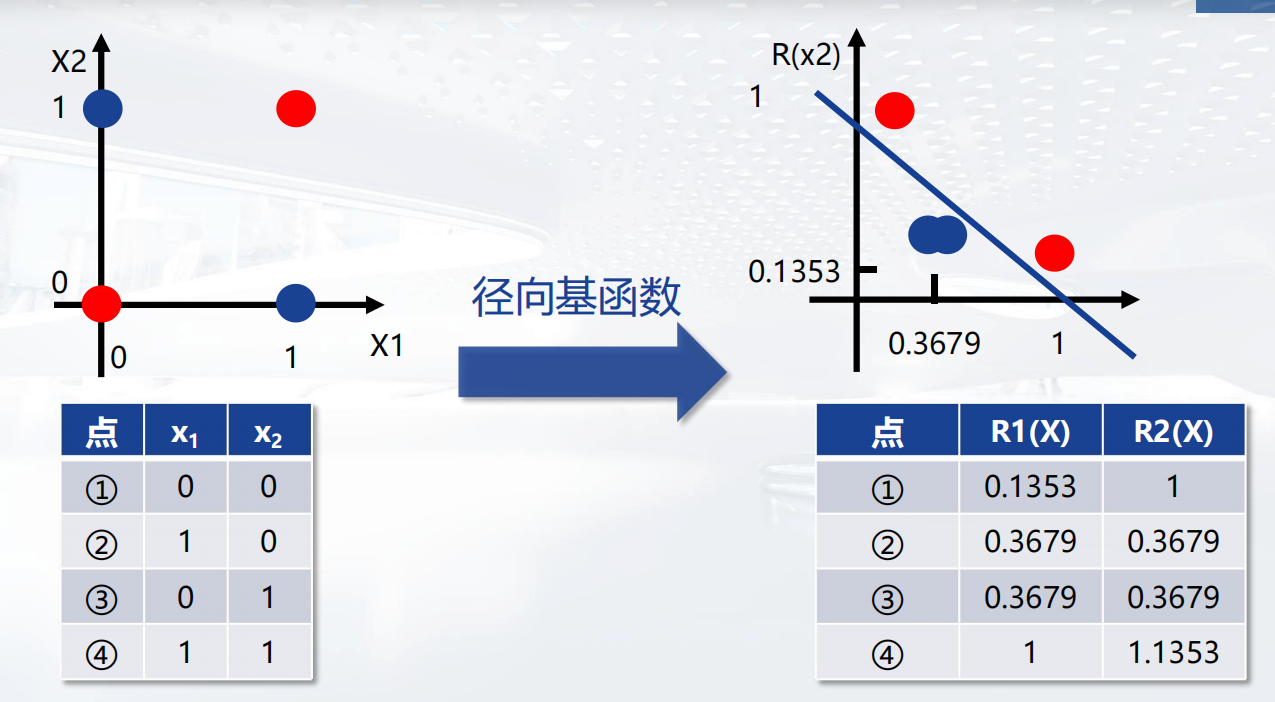
RBF神经网络学习算法
是一种单隐层前馈神经网络,它使用径向基函数作为隐层神经元激活函数,而输出层是对隐层神经元输出的线性组合。