ch3 参数估计
预备知识与记号
对于某个事物分为两类(a state of nature)
对于其特征x(feature vector),其类条件概率密度/似然(class-conditional density / likelihood)为
先验概率(prior probability)
后验概率(posterior probability)
对于独立同分布的一组变量
容易计算先验概率为
对于类条件概率分布:
有参数形式 没有参数形式(下一章内容)
比如服从高斯分布
目标
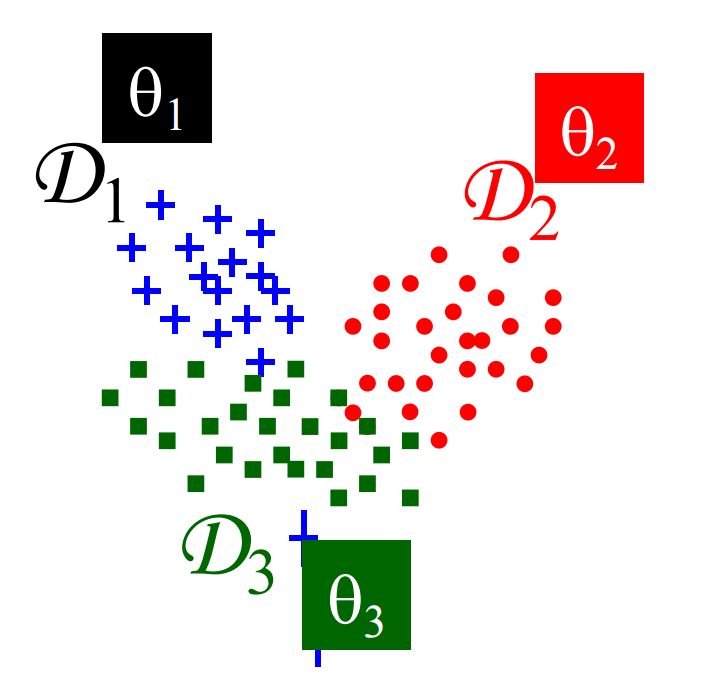
通过
概率与似然
概率:描述了参数已知时的随机变量的输出结果
似然:用来描述已知随机变量输出结果时,未知参数的可能取值。通过证据,对参数进行推断
最大似然估计:得到最可能的参数的过程。
极大似然估计
从特殊到一般,针对多次实验,用
此时我们的目标就是
通常使用对数似然函数
目标转化为
因为每个类都是独立的,所以从现在开始省略下标。
极大似然(ML)准则:
根据独立性假设,我们有:
似然函数:
极大似然估计:
经常转为对数似然:
计算极值:
正态分布的极大似然估计
- 情况1:均值未知,方差已知
- 情况2:均值未知,方差未知
情况1:均值未知,方差已知
推导可得到高斯分布的均值的极大似然估计为样本均值。
情况2:均值未知,方差未知
推导可得到高斯分布的均值的极大似然估计为样本均值,方差的极大似然估计为有偏样本方差,
贝叶斯估计
每个类独立的前提下,可以得出
问题公式化
(了解即可,我们这边考试不考)