ch1 机器学习绪论
1. 机器学习的定义
机器学习是这样一门学科:它致力于研究如何通过计算的手段,利用经验来改善系统自身的性能。“经验”通常以“数据”的形式存在,从“数据”中产生“模型”model的算法,即“学习算法”learning algorithm。
2. Label&Fearture
如何挑选一个西瓜?
西瓜的颜色、瓜蒂的形状、敲击的声音就是特征,而“好瓜”和“坏瓜”这两个判断就是标签。特征是做出某个判断的证据,标签是结论。
层次标签 hirerchical label
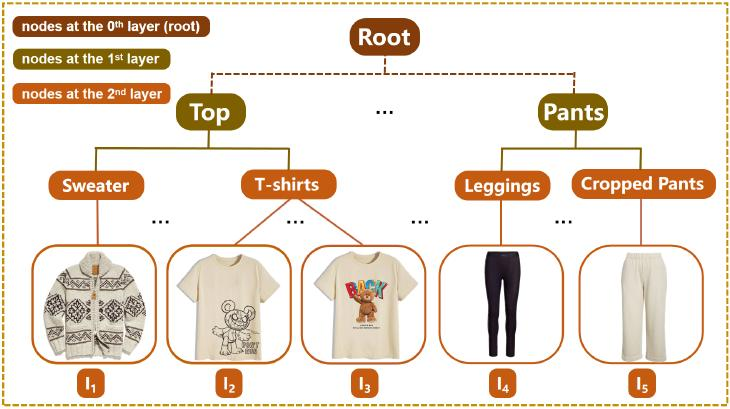
细粒度图像分类 fine-grained image classification

3. 机器学习框架 Machine Learning Framework
根据训练数据是否拥有标记信息,学习任务可以大致划分为两大类:“监督学习”(Supervised learning)和“无监督学习”(Unsupervised learning)。(機械学習:「教師あり学習」と「教師なし学習」)
除此之外还有……:
- Semi-supervised learning 半监督学习
- Reinforcement Learning 强化学习
- Active learning 主动学习
- ……
监督学习 Supervised Learning
训练数据含有标记的学习范式。从给定的训练数据集中学习出一个函数,当新的数据到来时,可以根据这个函数预测结果,最小化预测结果和真实标签的差异。监督学习的训练集要求是包括输入和输出,也可以说是特征和目标,训练集中的目标是人为标注的。
training data 训练数据/训练集,训练样本,特征,标签 
test data 测试数据/测试集,测试样本,特征,预测标签(classification) 
对于分类问题,我们想预测出他的种类;对于回归问题,我们想预测出一个数值。为了做出预测,需要各种各样的输入。
如何做出预测?
主要方法还是通过训练数据来训练出一个模型来估计参数,然后通过这些参数来对测试数据进行预测。这样当我们对测试数据做预测时能减少计算量,因为只需要估计一次参数,然后就可以用这个模型对所有测试数据进行预测。
方法例:
线性回归
其他方法:最近邻
对于最近邻方法,K不能太小也不能太大,太小会导致过拟合,太大则会欠拟合。
对比:
- 在计算量方面,上文两个方法有差异,最近邻方法需要储存所有的训练数据来计算;而线性回归只需要储存参数。
- 对于数据特征方面,NN有过拟合的风险;而线性回归可能会有偏差的风险。
无监督学习 Unsupervised Learning
人工标注类别成本太高,而且在缺乏足够先验知识情况下人工难以标注类别。 无监督学习的训练集没有人为标注的标签,直接自动对数据的的特征进行分析,发现数据之间的相似性。主要方法有聚簇(clustering),将数据分成由相似的样本组成的多个簇的过程,同一个簇的数据相似度高,不同簇之间数据相似度低。
正所谓“物以类聚,人以群分”(《战国策·齐策三》)。
半监督学习 Semi-supervised Learning
介于监督学习和无监督学习之间,训练数据同时包含有标记样本数据和无标记样本数据。他在训练时使用了少量的有标签数据和大量的无标签数据,提高模型性能。
半监督学习一览
- 约束聚类 Constrained Clustering
- 距离度量学习 Distance Metric Learning
- 基于流形的学习 Manifold based Learning
- 基于稀疏性的学习(压缩感知) Sparse based Learning (Compressed Sensing)
- 主动学习 Active Learning
- ……
约束聚簇 Constrained Clustering
在聚类过程中引入了额外的约束信息(必须连接、禁止连接),这些约束可以是用户指定的先验知识、领域规则或者数据本身所具有的特定关系。
主动学习 Active Learning
传统的监督学习算法被动地接受训练数据,主动学习与之相反,能够主动地从数据集中选择最有信息量的数据样本进行标注。其核心思想是通过最少的标注成本来获取最高的模型性能提升。
强化学习 Reinforcement Learning
智能体在环境中通过一系列行动与环境交互,根据环境反馈的奖励信号来学习最优策略,以最大化长期累积奖励。
其他框架……
- 多标记学习 Multi-label Learning
- 多实例学习 Multi-instance Learning
- 多实例多标记学习 Multi-instance multi-label Learning
- 迁移学习 Transfer Learning
- 深度学习 Deep Learning
4. 机器学习面临的挑战
处理复杂性
涉及众多变量时,我们如何应对这种复杂性而不至于陷入困境。
解决方法:
- 限制复杂性是一种方法。使用一个复杂度足以体现问题关键要素,但又不至于复杂到出现过拟合情况的模型。当我们选择的模型参数对已有数据拟合得非常好,但在新数据上表现很差(泛化能力不佳)时,就会发生过拟合现象。
- 降低维度是另一种可行的办法。显然,如果我们能找到办法将大量变量缩减为少量变量,事情就会变得更简单。
- 基于复杂性进行平均的贝叶斯方法。可以根据需要使用复杂的模型,但不要选择单一的参数值。相反,要对使用所有那些能较好地拟合数据且对于该问题合理的参数值所得到的预测结果进行平均。
优化与积分
通常需要为某些参数找出最佳值(这是一个优化问题),或者对许多合理的值求平均(这是一个积分问题)。当存在众多参数时,我们如何高效地完成这些操作呢。
可视化
要弄清楚正在发生的情况是很困难的,是用二维呢?还是三维呢?
维度灾难
通常是指在涉及到向量的计算的问题中,随着维数的增加,计算量呈指数倍增长的一种现象。
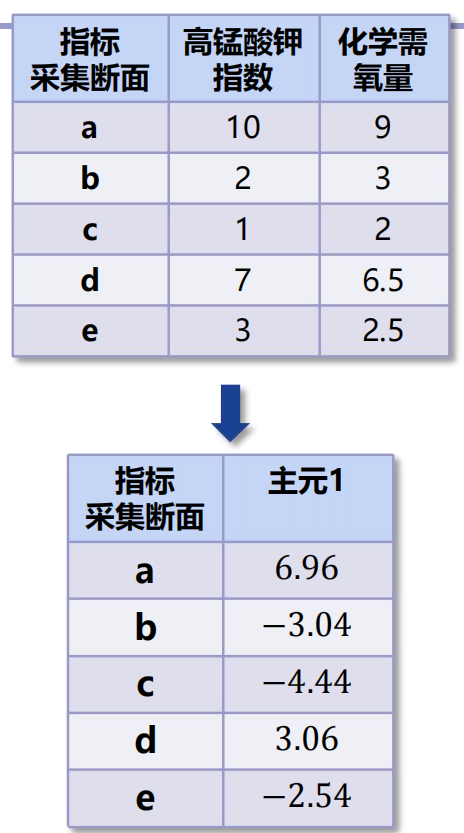
模型性能随着特征的增加先上升后下降。 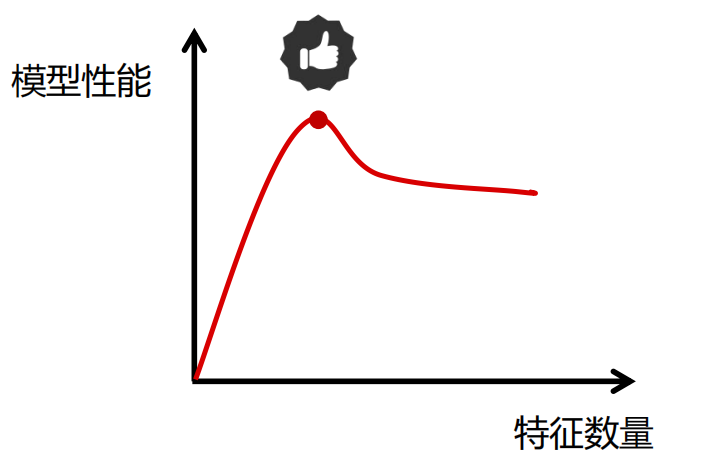
解决方法:主成分分析(PCA)
- 目标:最大化投影后的样本的方差(使得投影后的样本尽可能分散),使得某一维度的数值尽可能的小,另一个维度的数值尽可能的大。
- 思想:减少数据集的特征维数,同时尽可能地保留信息。
 算法伪代码:
算法伪代码:
- 将原始数据表示成矩阵X。
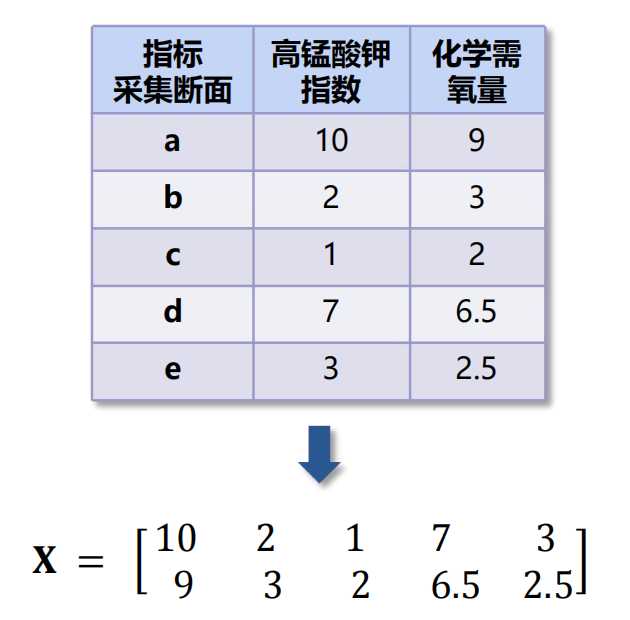
- 数据预处理。进行中心化处理,即减去均值。
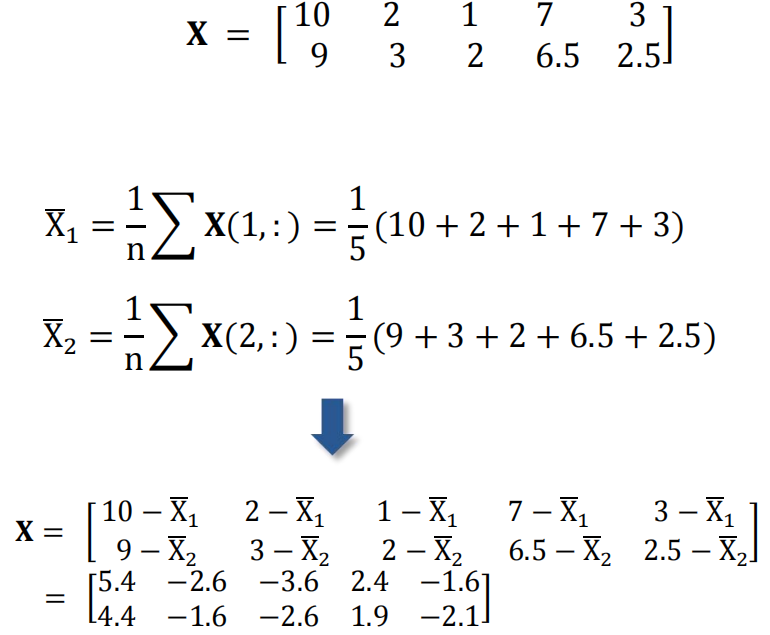
- 求出协方差矩阵
。 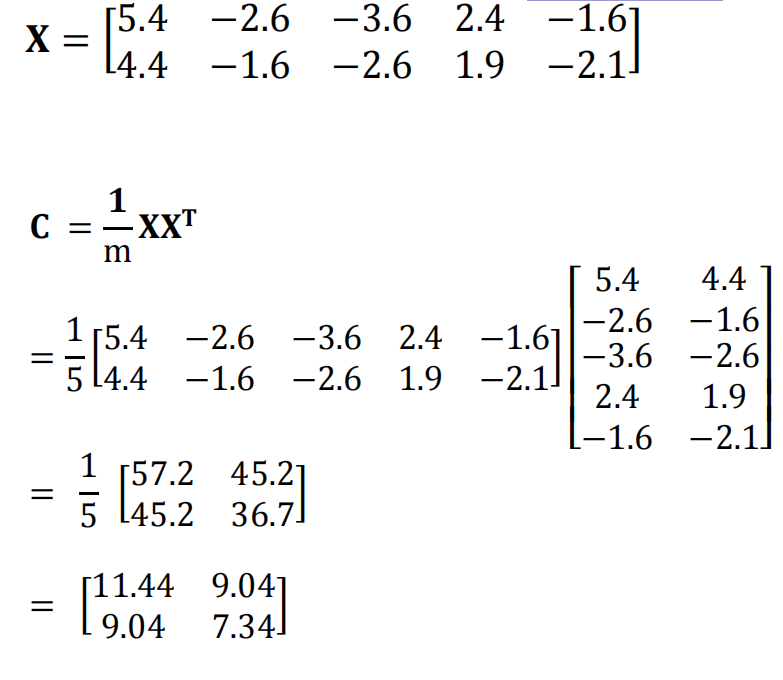
- 计算协方差矩阵的特征值和特征向量。

- 将特征向量按对应的特征值从上到下由大到小排列成矩阵,取其前K组成矩阵P。

- 计算
,得到的矩阵Y即为X降到K维后的数据。