ch10 聚类
写在前面……
博主是学数据科学与大数据技术的，所以这部分是和其他专业课有非常大的重叠，写的可能比较草率，这几个算法在博主所在的专业都考烂了
总览
- 原型聚类 K-means
- 密度聚类 DBSCAN
- 层次聚类 AGNES
聚类
簇 cluster：将数据分成由相似的样本组成的多个簇的过程
K-means
这是个NP-Hard问题，但是通过迭代和贪心策略能近似求解。
算法步骤
优点
原理直观，参数只有K，可解释性较强
缺点
对数据分布敏感，对K的选择敏感，对离群点敏感
关于原型聚类
- 亦叫做基于原型的聚类 prototype-based clustering
- 假设聚类结构能够通过一组原型刻画，在聚类中极为常见
- k均值算法，用原型向量刻画聚类结构
- 学习向量量化LVQ，用原型向量刻画聚类结构
- 高斯混合聚类，用概率模型表达聚类原型
DBSCAN
具有噪声的基于密度的聚类方法。先发现密度较高的点，然后把相近的高密度点逐步都连成一片，进而生成各种簇。
参数：
- 邻域半径R
- 邻域内点的最小数目MinPts
三种点
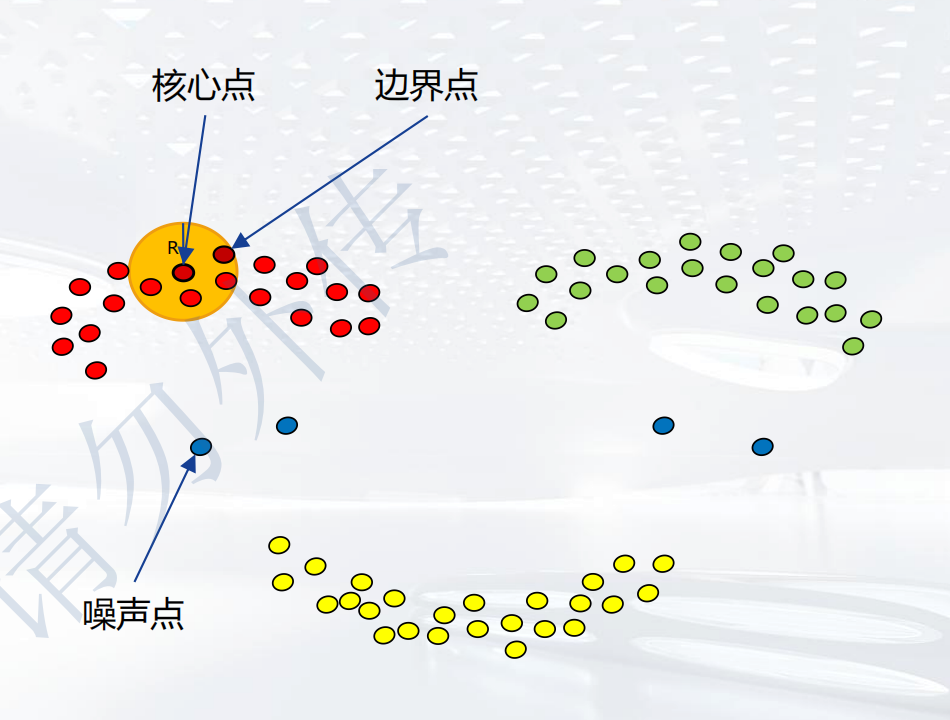
当邻域半径R内的点数不少于MinPts时，就是密集的，称之为核心点。
不属于核心点但是在某个核心点邻域内的点，称之为边界点。
既不是核心点也不是边界点的点，称之为噪声点。
四种点关系
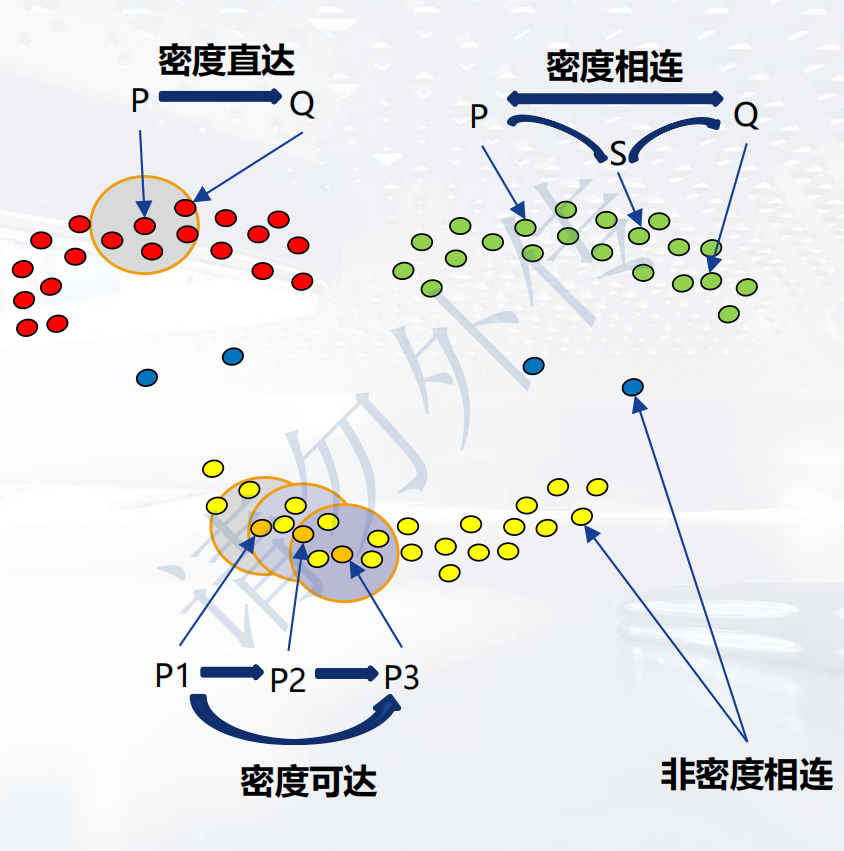
- 密度直达：如果P为核心点，Q在P的R邻域内，那么称P到Q密度直达。核心点到其自身密度直达。
- 密度可达：如果存在核心点P1,P2,…，Pn,且P1到P2密度直达，P2到P3密度直达，…，P(n-1)到Pn密度直达，Pn到Q密度直达，则P1到Q密度可达。（说白了就是两点之间存在一条密度直达的路径）
- 密度相连：如果存在核心点S，使得S到P和Q都密度可达，则P和Q密度相连。密度相连的两个点属于同一个聚类簇。
- 非密度相连：如果两个点不属于密度相连关系，则两个点非密度相连。
算法步骤
给定的邻域距离R和邻域最小样本个数。
- 遍历所有样本，找出所有满足R的核心对象的集合；
- 任意选择一个核心对象，找出其所有密度可达的样本并生成聚类簇；
- 从剩余的核心对象中移除2中找到的密度可达的样本；
- 从更新后的核心对象集合重复执行2-3步直到核心对象都被遍历或移除。
优点
- 自行确定簇的数目，不需要事先指定
- 可以对任意稠密数据集进行有效聚类
- 对异常点不敏感
缺点
- 调参复杂
关于密度聚类
- 亦称基于密度的聚类 density-based clustering
- 假设聚类结构能够通过样本之间的紧密程度确定
- DBSCAN，基于“邻域”参数来刻画样本分布的紧密程度
AGNES
层次聚类（Hierarchical Clustering），试图在不同层次对数据集进行划分，从而形成树形的聚类结构，既可以采用对数据集“自底向上”的聚合策略，也可以采用对数据集的“自顶向下”的分拆策略。
AGNES，AGglomerative NESting，凝聚层次聚类。
算法步骤
采用自底向上的聚合策略
- 首先将数据集中的每一个样本看作一个初始聚类簇
- 然后在算法运行的每一步中找出距离最近的两个簇进行合并（需要使用集合与集合的距离度量）
- 该过程不断重复，直至到达预设的聚类簇个数
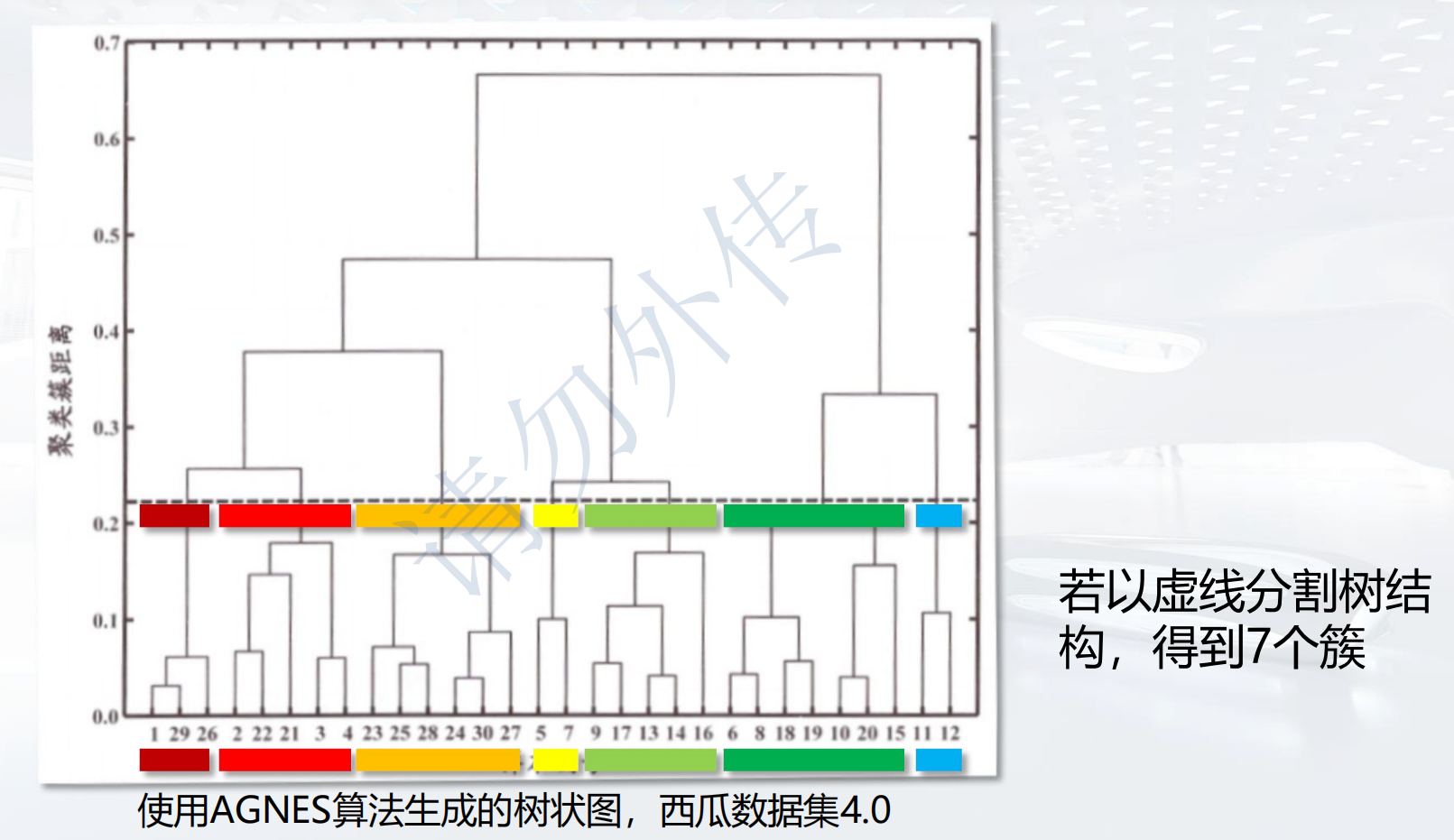最后会划分出类似这样的树，根据聚类需要选择截断位置并获得对应数量的簇。