ch2 贝叶斯决策论

预备知识与记号

对于某个事物分为两类（a state of nature）${\omega }_1,{\omega }_2$

对于其特征x（feature vector），其类条件概率密度/似然（class-conditional density / likelihood）为$p(x|{\omega }_1),p(x|{\omega }_2)$

$p(x)$称之为证据（evidence probability）

先验概率（prior probability）$p({\omega }_1),p({\omega }_2)$

后验概率（posterior probability）$p({\omega }_1|x),p({\omega }_2|x)$

观察前的决策

朴素决策：若是$p({\omega }_1)>p({\omega }_2)$，则选择${\omega }_1$，反之选择${\omega }_2$

在没有观察的情况下，选择先验概率大的哪个永远都是最好的决策。但先验概率缺少对数据的观测，不能借助数据本身的信息。

观察后的决策

根据观察，可以得到类条件概率密度分布$p(x|{\omega }_i)$与证据$p(x)$，可以贝叶斯定理得出后验概率（条件概率）

$$p({\omega }_i|x)=\frac{p(x|{\omega }_i)p({\omega }_i)}{p(x)}$$

贝叶斯定理：

$$p({\omega }_i|x)p(x)=p({\omega }_i)p(x|{\omega }_i)=p(x,{\omega }_i)=p({\omega }_i,x)$$

进而得出

$$p({\omega }_i|x)=\frac{p(x|{\omega }_i)p({\omega }_i)}{p(x)}$$

既

$$posterior=\frac{likelihood\times prior}{evidence}$$

其中归一化因子$p(x)$计算方法为

$$p(x)=\sum _{i=1}^{c}p({\omega }_i)p(x|{\omega }_i)$$

我们要做的是最大化后验概率，即

$$\mathcal{D}(x)=\arg \underset{{\omega }_i}{max}p({\omega }_i|x)$$

其中arg的意思是求最大值的对应的自变量。

特殊情况

• 等先验概率时：决策取决于哪个类条件概率密度更大
• 等类条件概率密度时：决策取决于哪个先验概率更大，退化为朴素决策

使用贝叶斯公式的前提

需要知道先验概率和类条件概率密度

贝叶斯决策是最优决策么？

对于决策，我们设定决策规则为：选择后验概率更大的那个类 那么对于错误，有 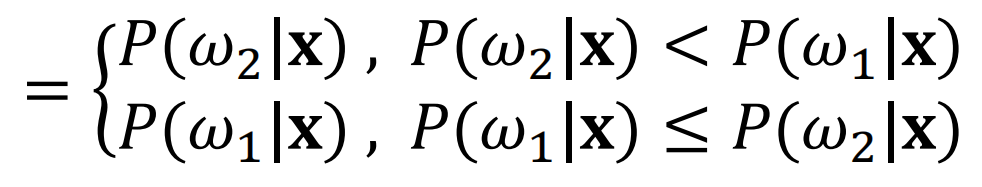我们定义

$$P(error|x)=min[P({\omega }_1|x),P({\omega }_2|x)]$$

为贝叶斯决策最小错误率。

广义贝叶斯决策规则

对于每个类别而言，误判的风险各不相同，所以风险也不一样。我们的目标是使风险最小化，因此对风险的误判同样会影响最终的决策结果。

我们定义损失函数:

$${\lambda }_{ij}=\lambda ({\alpha }_i|{\omega }_i)$$

其中${\alpha }_i$指采取的行动，${\omega }_j$指类别。 举个例子：

需要解决什么问题？

给定一个x，我们需要采取一个行动，而且做决策时需要最小化预期损失（风险）。预期损失和采取的行动有所关联，实际上的x的类别也是不确定的。

预期损失也有一个别名叫做条件风险，定义如下：

$$R({\alpha }_i|x)=\sum _{j=1}^c\lambda ({\alpha }_i|{\omega }_i)p({\omega }_j|x)$$

如果损失函数是0/1损失函数，即只有${\alpha }_i$是对应于${\omega }_j$的正确决策时，损失为0；否则为1。那么此时的预期损失即为贝叶斯决策最小错误率。

$$R({\alpha }_i|x)=P(error|x)$$

举个例子：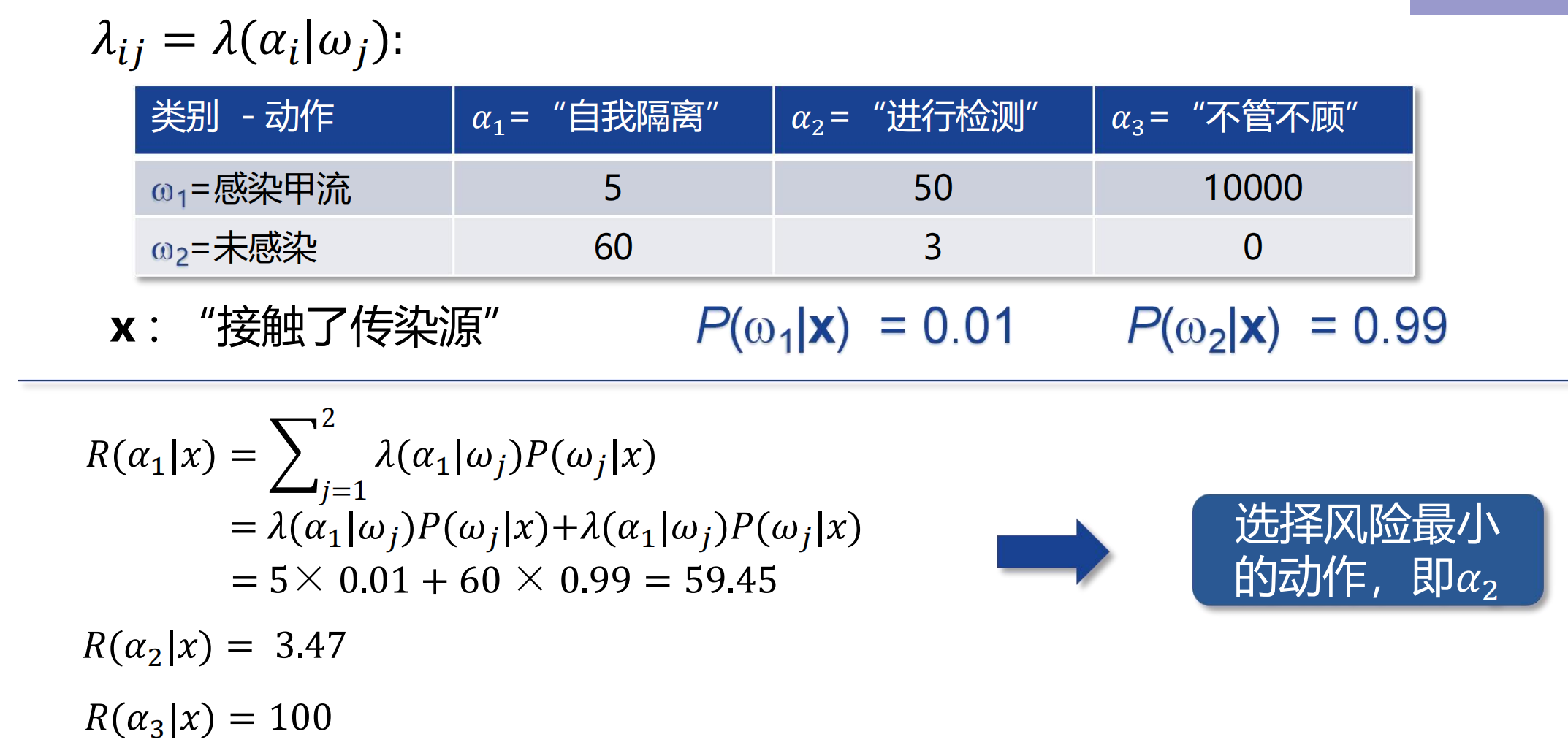

总结来说，我们的目标是：

$$\alpha (\mathbf{x})=\underset{{\alpha }_i\in A}{\arg min}R({\alpha }_i|\mathbf{x})=\underset{{\alpha }_i\in A}{\arg min}\sum _{j=1}^c\lambda ({\alpha }_i|{\omega }_j)P({\omega }_j|\mathbf{x})$$

总体风险（贝叶斯风险）:

$$R=\int R(\alpha (\mathbf{x})|x)\cdot p(x)dx$$

最优决策就是使得贝叶斯风险最小的决策。

二分类问题

如果$R({\alpha }_2|x)>R({\alpha }_1|x)$，采取行动${\alpha }_1$，反之${\alpha }_2$。

根据一系列数学推导，在损失函数是0/1损失函数的情况下，最小错误率贝叶斯决策（选择后验概率大的）是最小风险贝叶斯决策（选择贝叶斯风险小的）的特例。

判别函数

判别函数适用于多分类问题。对于每个类别，都有一个判别函数$g_i(x)$与之对应。当对于任意的$i\ne j$，都有$g_i(x)>g_j(x)$时，我们认为${\omega }_i$是正确的类别。 定理：如果$f(x)$是单调递增的函数，那么$f(g_i(x))$也可以作为判别函数。

决策区域定义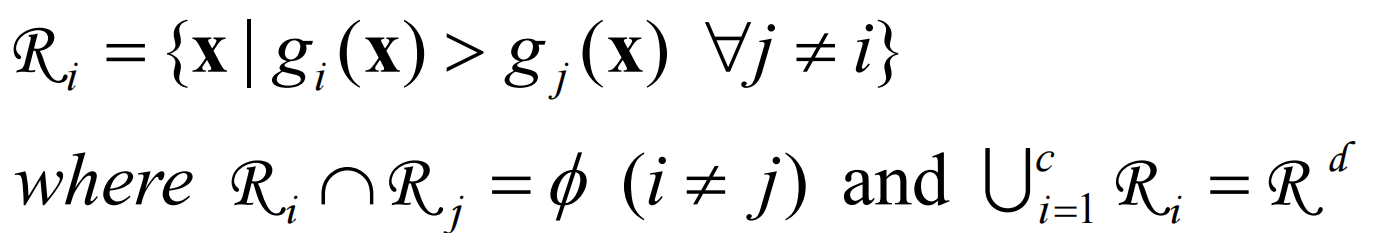： c个判别函数会产生c个决策区域，决策边界是决策区域之间的边界。

正态分布下的贝叶斯决策规则

各种数学量的计算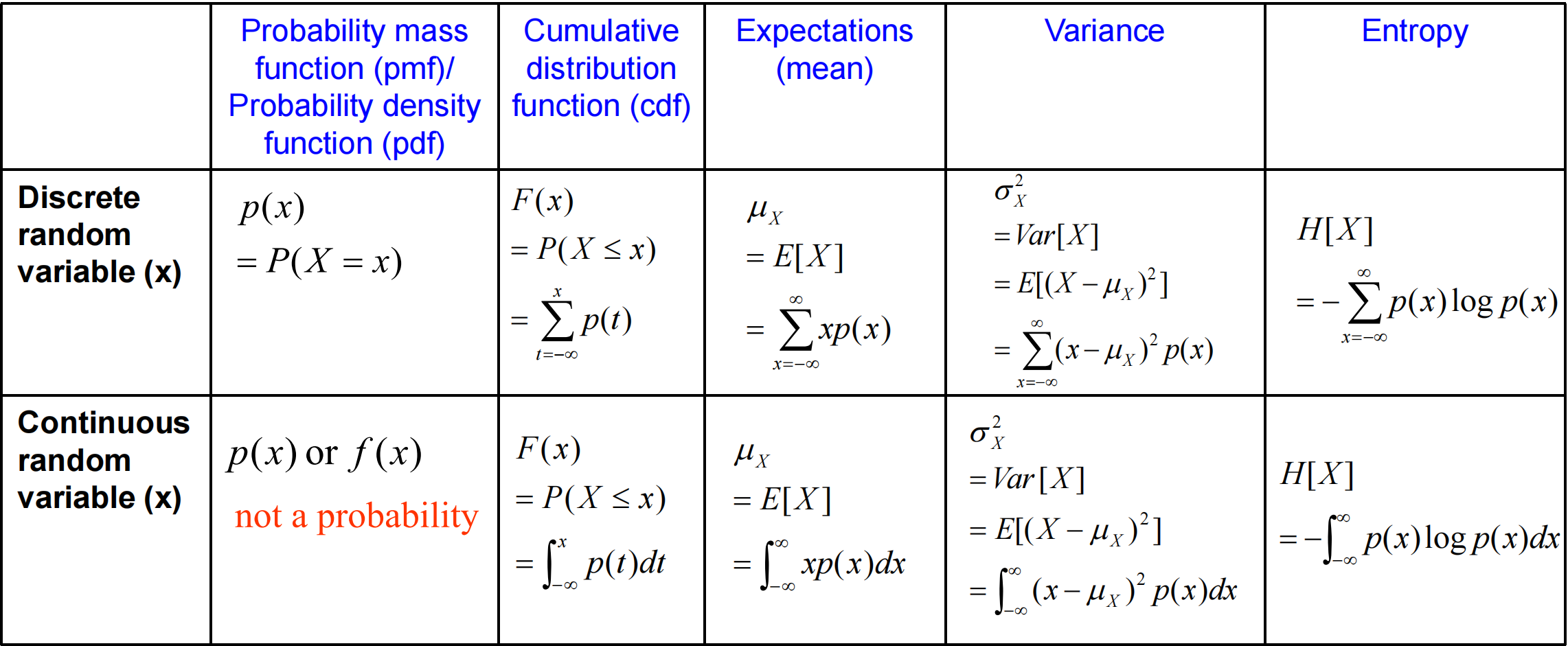： （后边及其变态 我就不写了 考了这分我直接不要了）

高斯密度划分函数

• 情况1
  • ${\mathbf{\Sigma }}_i={\sigma }^2\mathbf{I}$
  • 类别以不同均值为中心，且它们的特征分量两两独立且具有相同方差。
• 情况2
  • ${\mathbf{\Sigma }}_i=\mathbf{\Sigma }$
  • 类别以不同均值为中心，但具有相同的方差。
• 情况3
  • 任意的
  • ${\mathbf{\Sigma }}_i\ne {\mathbf{\Sigma }}_j$

补充：机器学习评价指标

1. 正确率（accuracy）

   $$\frac{TP+TN}{TP+FP+FN+TN}$$

2. 错误率（error rate）

   $$\frac{FP+FN}{TP+FP+FN+TN}$$

3. 精度（precision）

   $$\frac{TP}{TP+FP}$$

4. 召回率（recall）

   $$\frac{TP}{TP+FN}$$

5. 精度-召回率曲线（PR曲线）：召回率和精度之间通常是此消彼长的关系。

6. AP（平均精度）

   PR曲线的积分。

   $$AP={\int }_0^{1}P(R)dR$$

   AP不会大于1，AP值越大模型性能越好。优秀的某型在召回率增长的同时，精度也保持在较高水平。

7. mAP（平均平均精度）：对于多个类别，将所有类别的AP求平均。

8. F-score

   $$F=\frac{(1+{\beta }^2)\times precision\times recall}{{\beta }^2\times precision+recall}$$

   通常$\beta =1$，此时称为F1-score。

9. ROC曲线与AUC

   真正率（TPR）与假负率（FPR）。

   $$TPR=\frac{TP}{TP+FN}，FPR=\frac{FP}{TN+FP}$$

   以假负率为横轴，真正率为纵轴作图，得到的曲线即为ROC曲线。ROC下的面积即为AUC，面积越大，模型性能越好。ROC曲线越光滑，模型过拟合的程度越低。

10. IoU（交并比）

    $$IoU=\frac{A\cap B}{A\cup B}$$

11. Top1与Topk

    对一张图片，模型给出的识别概率中（即置信度分数），分数排名前K位中包含有正确目标（正确的正例），则认为正确。