ch4 非参数估计

总览

• Parzen窗口估计
• KNN估计

对于一些后验概率的概率分布中没有参数，这种情况就得让数据自己说话，也就是非参数估计。

Parzen窗口估计

目标

• 估计类条件概率密度 $p(x|{\omega }_i)$
• 估计后验概率 $p({\omega }_i|x)$

密度估计

一个向量 $x$ 的落入某个区域 $R$ 的概率密度估计为：

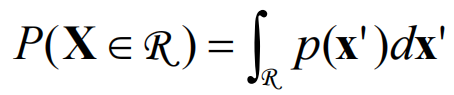
假设$p(x)$是连续的，而且$R$非常小，可以近似得到：

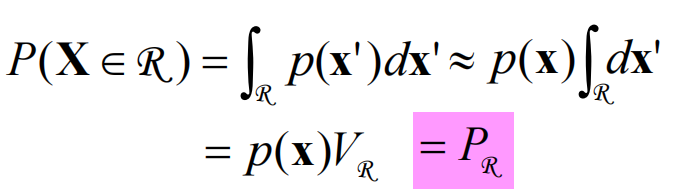
K个样本落入区域遵循二项分布：

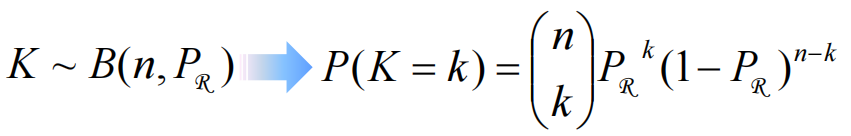
数学期望：

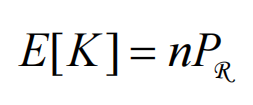
结合上边两个式子可以得出$p(x)$：

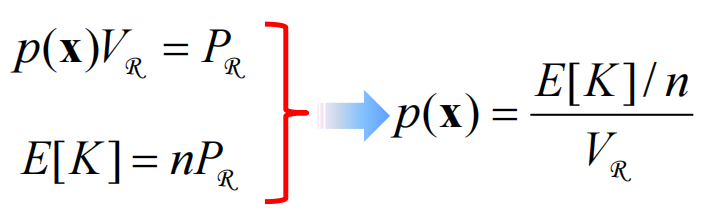
用$k_R$表示窗口函数内实际样本数量，可以近似计算出：

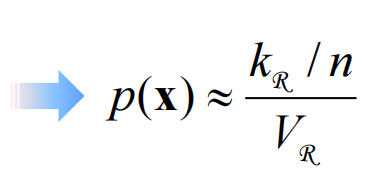
使用n作为下标（核心公式）：

我们希望：

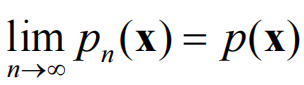
为了实现逼近，需要：

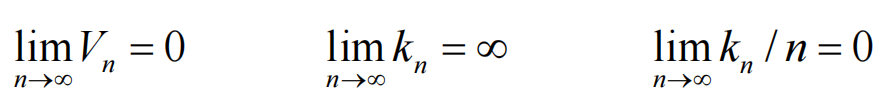
固定Vn计算kn，即为Parzen窗口估计的核心。Rn是一个d维的超立方体，其边长为hn，Vn实际上是“测度”，计算方式是：

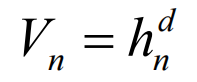
窗函数

通过定义如下的窗函数，得到落在窗中的样本数:

定义了一个d维空间中，中心点在原点边长为1的超立方体。

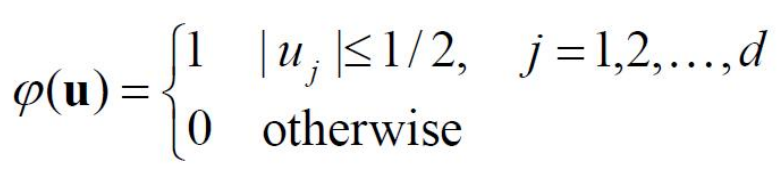
如果是边长为hn的超立方体，则：

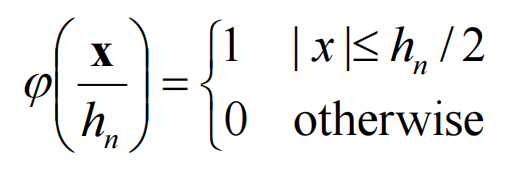
中心点不在原点则：

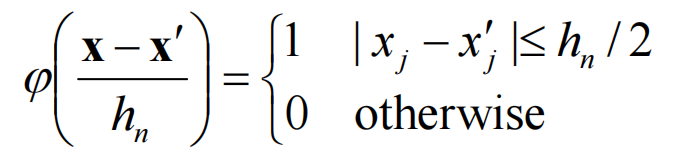
这里的函数值1表示落入了超立方体中。

kn：落在超立方体的总样本数。

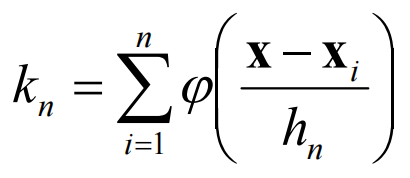
与上文的核心公式结合获得Parzen概率分布函数：

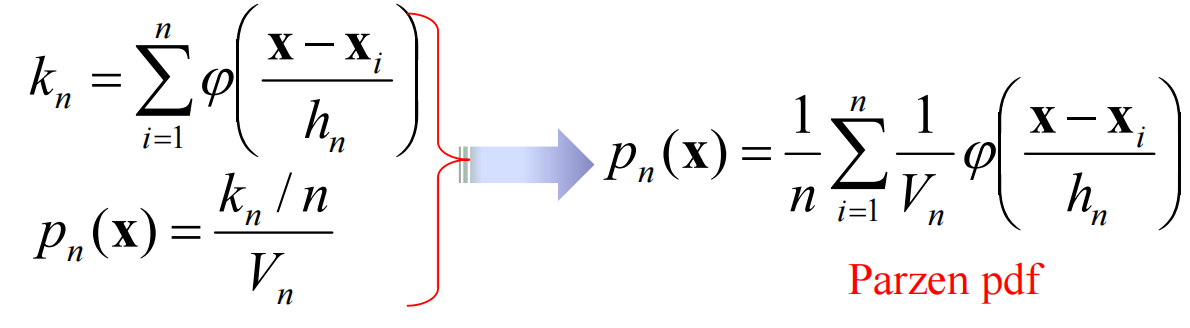
其中$\varphi (u)$不局限于超立方体，可以是任意窗函数，只要符合如下要求即可：

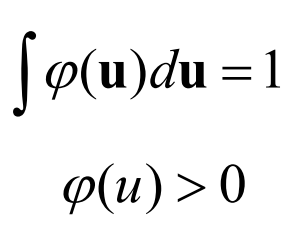
根据窗函数$\varphi (u)$定义${\delta }_n(x)$，代入核心公式中得到：

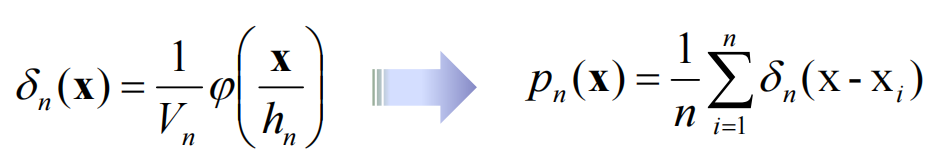
为了保证收敛，需满足：

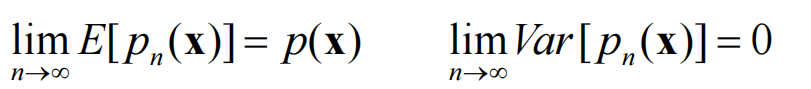
还有额外限制：

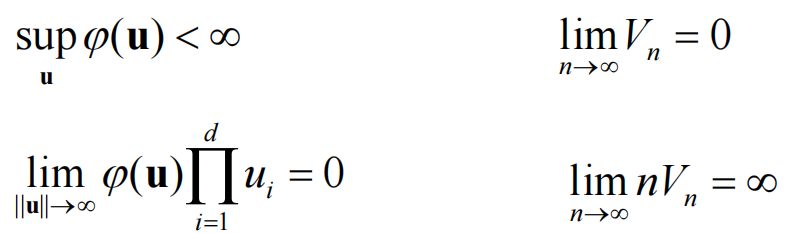
Vn在n趋近正无穷的时候需要收敛到0，但是收敛速度不能比1/n快，我们选择：

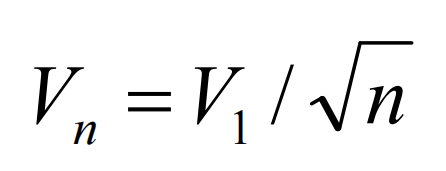
如此，初始值V1的选取很重要。

KNN估计

同样使用上文核心公式，但是固定kn然后决定Vn。为了保证收敛，同样有选取要求：

对于KNN，有

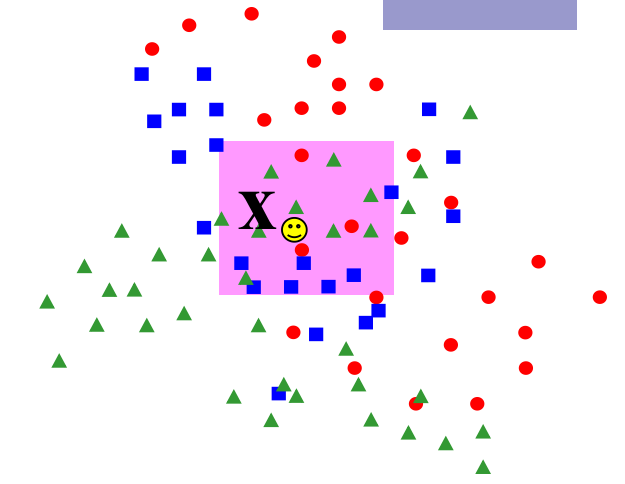
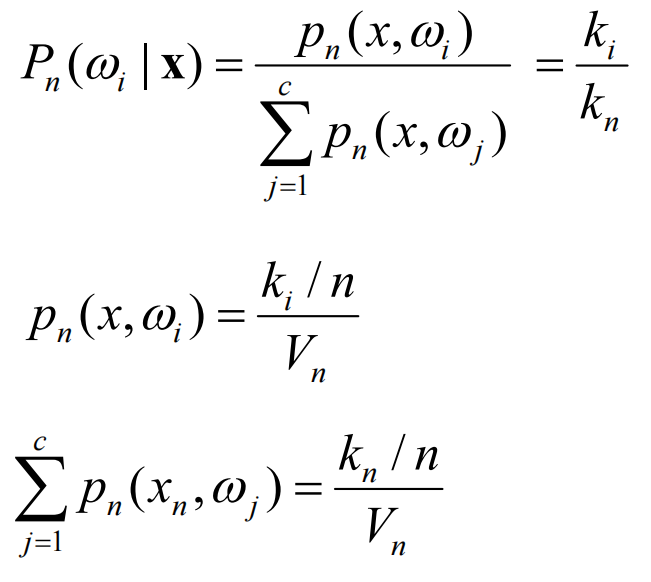
KNN分类技术

闵可夫斯基距离

• n=1,曼哈顿距离
• n=2,欧氏距离
• n趋向无穷，切比雪夫距离

余弦相似度/余弦距离

略

K近邻算法

• 给定输入实例
• 选择合适的距离公式
• 算出该实例与所有已知实例的距离
• 根据算出的距离，找出与输入实例距离最小的K个已知实例（K一般是奇数，K = 1时为最近邻算法）
• 做分类：一般是多数表决，即由输入实例的k个邻近的的多数类决定输入实例的类。

特点

懒学习（不给测试机不学）

优点

• 原理简单
• 可解释性强
• 参数只有K
• 无需训练过程

缺点

• 储存消耗
• 计算开销
• K值不好确定
• 不好找到一个合适的距离公式
• 不相关的特征和噪声可能会非常有害